隠れマルコフモデルは、工学、生物学、経済学など様々な領域で使われている機械学習モデルです。

状態空間モデルにおける状態が離散的なモデルでもあり、実用的なアプリケーションとして、オンラインの手書き文字認識や音声認識、またセンサー類のデータの状態推定や異常検知など、その応用範囲は幅広く、現在でも多くのシーンで利用されているアルゴリズムです。

今回は隠れマルコフモデルのパラメータの推定を、EMアルゴリズムを使ってやっていきます。

本記事の内容

• 隠れマルコフモデルをEMアルゴリズムで学習してパラメータを推定
• Baum-Welch（バウム・ウェルチ）の アルゴリズム

隠れマルコフモデル(HMM)の復習

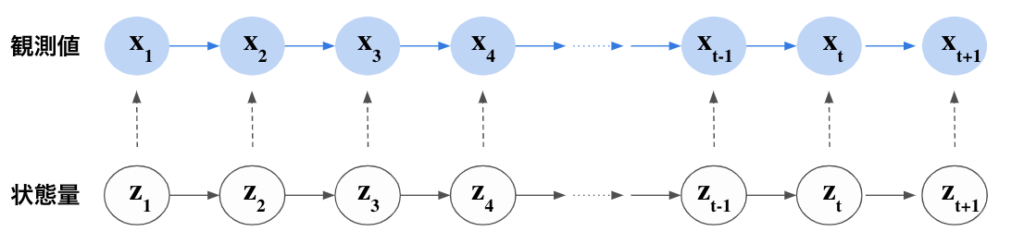
隠れマルコフモデルの、潜在変数$z$と観測値$x$の関係性はこのようになっています。

観測値$x$は、状態量を$z$に条件付けられており、状態量によって観測値が決まるようなモデルになっています。HMMモデルの詳しい説明は、下記の記事をご覧ください。

[

隠れマルコフモデル(HMM)の理論をわかりやすく解説

隠れマルコフモデルは、離散的な状態を仮定する、いわゆる状態空間モデルのアルゴリズ…](https://disassemble-channel.com/the-theory-of-hidden-markov-model-hmm/)

隠れマルコフモデル(HMM)におけるEMアルゴリズムの準備

今回は、観測値$\bm{X} = \{ \bm{x_1}, \bm{x_2}, \dots, \bm{x_n} \}$が与えられている時に、EMアルゴリズムによって最適なモデルパラメータ$\bm{\theta}$の学習をしていきます。

今回扱い隠れマルコフモデルにおいては、潜在変数$\bm{Z} = \{ \bm{z_1}, \bm{z_2}, \dots, \bm{z_n} \}$があり、潜在変数によって観測値が与えられているとされる、潜在変数モデルとなっています。

確率モデルのパラメータ推定の1つの手法として、最尤推定(Maximum Likelihood Estimation)があります。

最尤推定は、尤度関数$p(\bm{X} | \bm{\theta})$を最大化するために、パラメータごとに偏微分を行い、各パラメータの最尤解を求める手法でした。

一方で、隠れマルコフモデルや状態空間モデルなど、潜在変数が介在するような確率モデルの場合には、一般的に尤度関数 $p(\bm{X} | \bm{\theta})$を最適化することが難しく、別の手法を考える必要性があります。

EMアルゴリズムでは、$p(\bm{X} | \bm{\theta})$を考えるのではなく、潜在変数$\bm{Z} $と観測値$\bm{X} $の同時分布を考え、その同時分布を最適化することで、最尤推定を適応する手法です。

具体的には、下記のような変形を行い、右辺の最適化を考えます。

[

【機械学習】EMアルゴリズムをゼロから理解する

EMアルゴリズム(expectation maximization algori…](https://disassemble-channel.com/em-algorithm/)

\begin{equation}
p(\bm{X} | \bm{\theta}) = \sum_Z p(\bm{X}, \bm{Z} | \bm{\theta}) 
\end{equation}

具体的には、こちらの記事を参考にしてください。

EMアルゴリズムで隠れマルコフモデル(HMM)を学習する

隠れマルコフモデルをEMアルゴリズムで学習する場合、このアルゴリズムをBaum-Welch（バウム・ウェルチ）の アルゴリズムと呼ばれています。

EMアルゴリズムでは、EステップとMステップを交互に繰り返しながら、最適なパラメータを学習する手法です。

Eステップでは、パラメータを固定した状態で、潜在変数$\bm{Z}$の事後確率$p(\bm{Z} | \bm{X}, \bm{\theta^{old}})$を求めます。

次のMステップでは、Eステップで求めた事後確率$p(\bm{Z} | \bm{X}, \bm{\theta^{old}})$を用いて、次の$\mathcal{Q}$関数を最小化するようなパラメータ$ \bm{\theta}$を見つけます。

\begin{equation}
\mathcal{Q}(\bm{\theta}, \bm{\theta^{old}}) = \sum_{Z} 
p(\bm{Z} | \bm{X}, \bm{\theta^{old}}) ln p(\bm{X}, \bm{Z} | \bm{\theta})
\end{equation}

HMMにおけるBaum-Welchの アルゴリズム

いよいよ、隠れマルコフモデルにおけるEMアルゴリズムの内容に入っていきましょう。

まず、簡単のため、次のような変数を導入します。これらの変数の導入は、いきなり登場し、面食らってしまうかもしれせんが、後続の計算を簡単にするための仕組みです。なので、今の段階では天下り的にこういうものだと思ってください。

$\gamma(\bm{z_n}) $: 潜在変数 $\bm{z_n}$の周辺事後分布

潜在変数$\bm{z_n}$の周辺事後分布を$\gamma(\bm{z_n}) $として導入します。

\begin{equation}
\gamma(\bm{z_n}) = p(\bm{z_n} | \bm{X}, \bm{\theta^{old}})
\end{equation}

$\xi(\bm{z_n}, \bm{z_{n-1}})$: 潜在変数 $\bm{z_n}, \bm{z_{n-1}}$の同時周辺事後分布

\begin{equation}
\xi(\bm{z_n}, \bm{z_{n-1}}) = p(\bm{z_n} , \bm{z_{n-1}} | \bm{X}, \bm{\theta^{old}})
\end{equation}

$\gamma(z_{nk}) $: 潜在変数 $\bm{z_n}$の周辺事後分布

この辺り、周辺事後分布の期待値を表現します。

$\xi(z_{n-1, j}, z_{nk})$: 潜在変数 $\bm{z_n}$の周辺事後分布

ここでもこの期待値の表現を書きます

ここまでで数式の導入が完了しました。次に、これらの導入した数式を用いて、最適化する(2)式の$\mathcal{Q}$関数を表現していきましょう。

結論から先に書いてしまうと、先ほど導入した4つの数式を用いると、(2)の$\mathcal{Q}(\bm{\theta}, \bm{\theta^{old}})$は次のように書くことができます。

\begin{equation}
\mathcal{Q}(\bm{\theta}, \bm{\theta^{old}}) = 
\sum_{k=1}^{K} ln  \pi_k

\gamma(z_{1k})
\end{equation}