ガウス混合分布(Gaussian Mixture Distribution)は、複数のガウス分布を足しわせた確率分布で、この確率分布を扱う機械学習モデルを、ガウス混合モデル(Gaussian Mixture Model)といいます。

混合ガウス分布を用いることで、通常のガウス分布では表現できないような、山が2つあるような多峰性の分布を表現することができたり、複数の確率分布を統合した確立モデルを考えることができ、非常に実務ではよく利用される確立モデルとなっています。

ガウス混合モデルも実用上非常によく利用されることがありますが、この混合モデルのフィッティングするには、大きく2つEMアルゴリズムによる最尤推定を行う手法と、ベイズ推論の枠組みを使う方法の2つがあります。

今回は、この混合モデルを学習する上で、ベイズ推論の枠組みでガウス混合モデルの学習とクラスタリングを行う手法を解説します。

特に、MCMC(マルコフ連鎖モンテカルロ法)と呼ばれる手法で、確率分布を学習する手法について解説をします。

EMアルゴリズムを用いる手法や、変分推論による学習手法などもありますが、それらについても別の記事で紹介しているので、そちらをご覧ください。

本記事の内容

• ガウス混合モデル、ガウス混合分布について分かりやすく解説
• MCMCを用いてガウス混合モデルをフィッティング
• ガウス混合モデルでデータをクラスタリングする

ガウス混合モデルをベイズの枠組みで定義する

何らかのデータの分布を表現する確立モデルを考えるには、生成モデル(generative model)という考え方を利用するのが良いです。

生成モデルとは、データ全体を構成する1つ1つのデータが、確立的にどのような経路を辿って、データが生成されたかを考えることで、モデルを定式化する考え方です。

定式化すると、ラベルの確率変数とその実現値を$Y, y$ 、データの確率変数とその実現値を$X, x$とした時、生成モデルは、$p( x | y)$を生成する問題となります。

一方、生成モデルとは別に、データ点からそのラベルを推論する、つまり$p( y | x)$を予測する問題を、識別モデルと呼びます。

この辺りは、ひとまず置いておいても、ガウス混合モデルを考える上では、生成モデルの考え方で、考えるとうまくモデルを構築することができます。

ガウス混合モデルの生成モデルを考える

では、ガウス混合モデルの定式化を考えていきます。

例えば、今回はガウス混合モデルで次のようなデータを表現することにします。

データは色付けして各クラスを示していますが、実際には、これらのクラスは分かっておらず、データから決定したいとします。生成モデルでは、これらのデータがどのような経緯で生成されたかを示す分布です。

混合ガウス分布の生成モデルは、具体的に次のように考えます。

混合ガウスモデル(GMM)における生成モデルの流れ

• 1. ある1つのデータ$x_n$に着目し、その点がどのクラスタに所属するかが確立的に決定される（これを$\bm{s_n}$で表現するとする)
• 2. そのクラスが属するガウス分布 $\mathcal{N}_k$ によって、$x_n$の値が確立的に決定される
• 3. $1 \sim N $全てのデータにおいて、上のステップ1, 2の過程が繰り返され、全てのデータNが決定される

このように定式化することで、混合ガウスモデルがうまく表現できます。

ここまでの流れをまとめると以下になります。

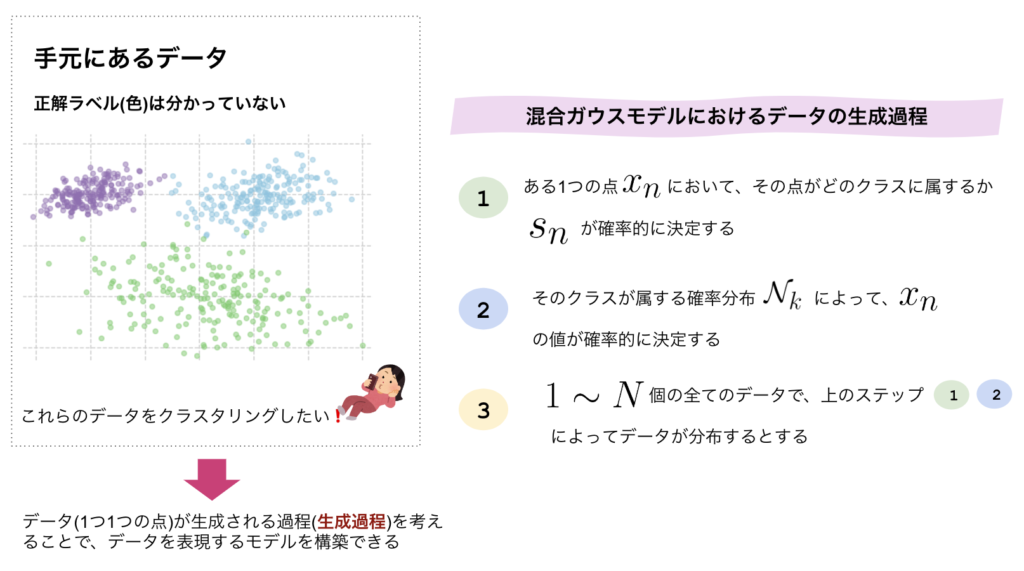
ここまでで、全体の生成モデルの流れをざっくりと考えてきました。しかし実際に統計・機械学習モデルとして考えるためには、これらを定式化する必要性があります。この定式化するには、どのようにしていくのでしょうか。

ガウス混合モデルのベイズ推論での定式化

それでは、ガウス混合モデルの定式化に入っていきます。

まず先ほど考えた生成モデルにおいて、最初に考えやすいところから定式化していきましょう。

まず、上記の生成モデルにおいて、クラスごとに$K$個のガウス分布を過程しました。そのため、この$K$個のガウス分布を定式化してみます。

あるクラス$k$における、ガウス分布は次のように表現できます。

\begin{equation}
\begin{split}
p(\bm{x_n} | \bm{\theta_k}) = \mathcal{N}(\bm{x_n} | \mu_k, \Sigma_k)
\end{split}
\end{equation}

ここで、左辺の$\bm{\theta_k}$は、$\bm{\theta_k} = \mu_k, \Sigma_k$ですが、一般化のためにこのように書きました。

また、$\bm{s_n}$について考えていきましょう。$\bm{s_n}$も確率変数として考えます。$\bm{s_n}$は、あるデータ$\bm{x_n}$が、クラス$k$に属するかどうかを表現する変数で、1-of-K表現で書くことができます。

よく、$\bm{s_n}$のような、何番目の数が選ばれるかを示す確率変数は、次のようにパラメータ$\bm{pi}$を用いたカテゴリカル分布で表現できます。

\begin{equation}
\begin{split}
p(\bm{s_n} | \bm{\pi}) = Cat(\bm{s_n} | \bm{\pi})
\end{split}
\end{equation}

この$\bm{\pi}$は、どのクラスタ$k$が選ばれやすいかを示す変数で混合比率と呼ばれることが多いです。ここで、この混合比率は、データから学習する必要性があるので、ここも確率変数として、表現したいです。

(2)のようなカテゴリカル変数のパラメータ$\bm{\pi}$の分布は、ディリクレ分布として次のように表現されることが多いので、今回もディリクレ分布を導入してみます。

\begin{equation}
\begin{split}
p(\bm{\pi}) = Dir(\bm{\pi} | \bm{\alpha})
\end{split}
\end{equation}

これらをまとめると、最終的な同時分布(joint distribution)はこのようになります。

ベイズ推論による混合ガウスモデルの同時分布

\begin{equation}
\begin{split}
p(\bm{X}, \bm{S}, \bm{\theta}, \bm{\pi}) &= p(\bm{X} |  \bm{S}, \bm{\theta}) p(\bm{S} | \bm{\pi}) p(\bm{\theta})  p(\bm{\pi}) \\
&= \biggl  \{ 
\prod_{n=1}^N
p(\bm{x_n | \bm{s_n}, \theta{}}) p(\bm{s_n} | \bm{\pi})
 \biggl  \}
\biggl  \{
\prod_{k=1}^K p(\bm{\theta}_k) 
\biggl  \}
p(\bm{\pi}) 

\end{split}
\end{equation}

ここで、$\bm{S}$は、$\bm{s_n}$の集合として定義しています。

(4)式により、考えている確率モデルの同時分布を得ることができました。同時分布の形をまず考えることが、考えている確率分布から様々な操作を行う1stステップなので、(4)でやっと一段落です。

ここで、(4)における確率変数は、$\{ \bm{X}, \bm{S}, \bm{\theta}, \bm{\pi} \}$ですが、$\bm{X}$は観測値で、実際に得ることができているため、求めるべき確率変数は、$\{ \bm{S}, \bm{\theta}, \bm{\pi} \}$となっています。

MCMCを用いてガウス混合モデルをフィッティング

ここで、Mcmcを使って、がうう混合モデルをフィッティングする内容について記載する.